Model-Order Reduction Optimization

I completed this work in undergrad as part of an independant research project under Pr. Alessandro Parente (Combustion and Robust Optimization Group, ULB).

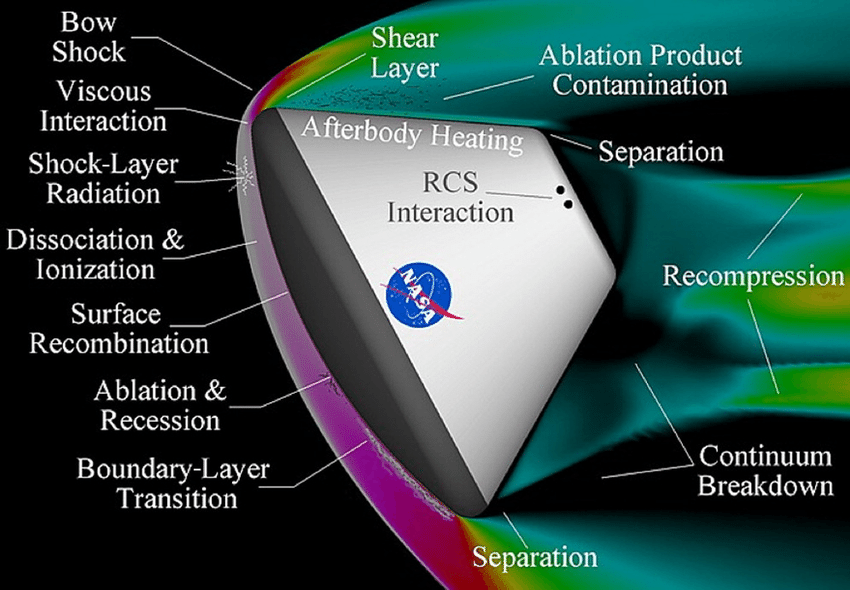
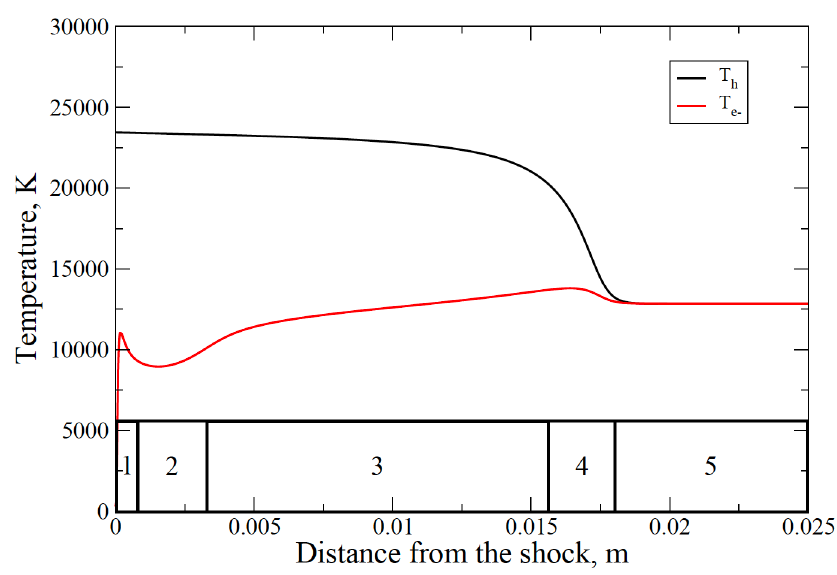
From physics, we understand that the thermochemical phenomena associated with a spacecraft re-entering the atmosphere can be divided into five distinct regions (see figure). Developing a single model that accurately accounts for all chemical interactions within these regions is challenging, as it would likely be highly inaccurate due to its broad generalizations. Therefore, we need to isolate those regions from the data so we could apply our more accurate model. The dataset used for this work came from an Argon Collisional-Radiative chemical model for atmospheric re-entry conditions simulated using a 1D shock tube (31 excited levels for Ar, 2 excited levels for Ar+, and 2 temperatures).

To achieve this, I implemented and compared clustering algorithms and ended up using Local Principal Component Analysis (L-PCA) clustering which organizes data based on their PCA reconstruction error. I conducted sensitivity analyses on various cluster initialization techniques, including some well-known clustering methods like K-means and spectral clustering. Following these analyses, we successfully assigned each data point to a cluster.

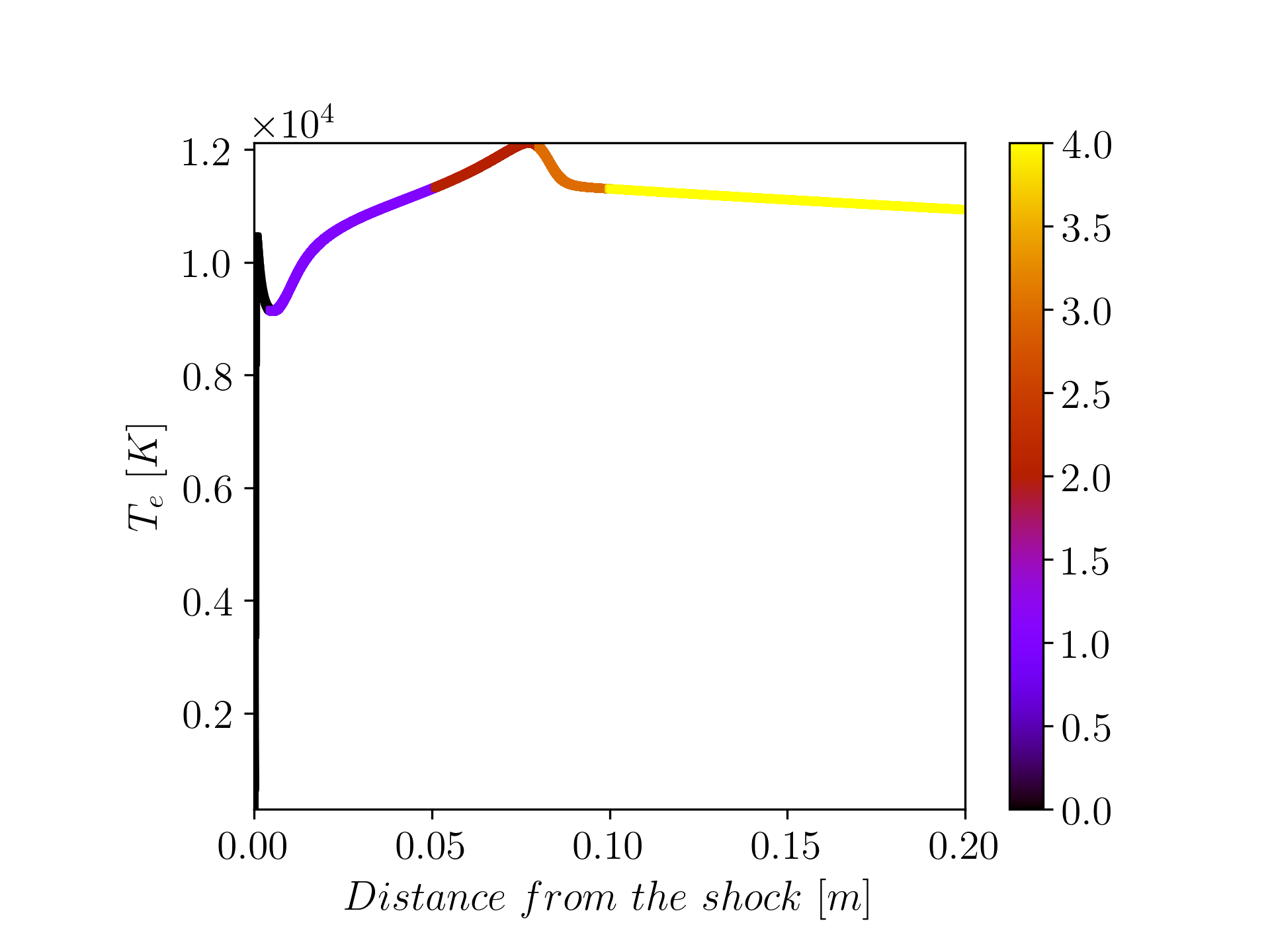
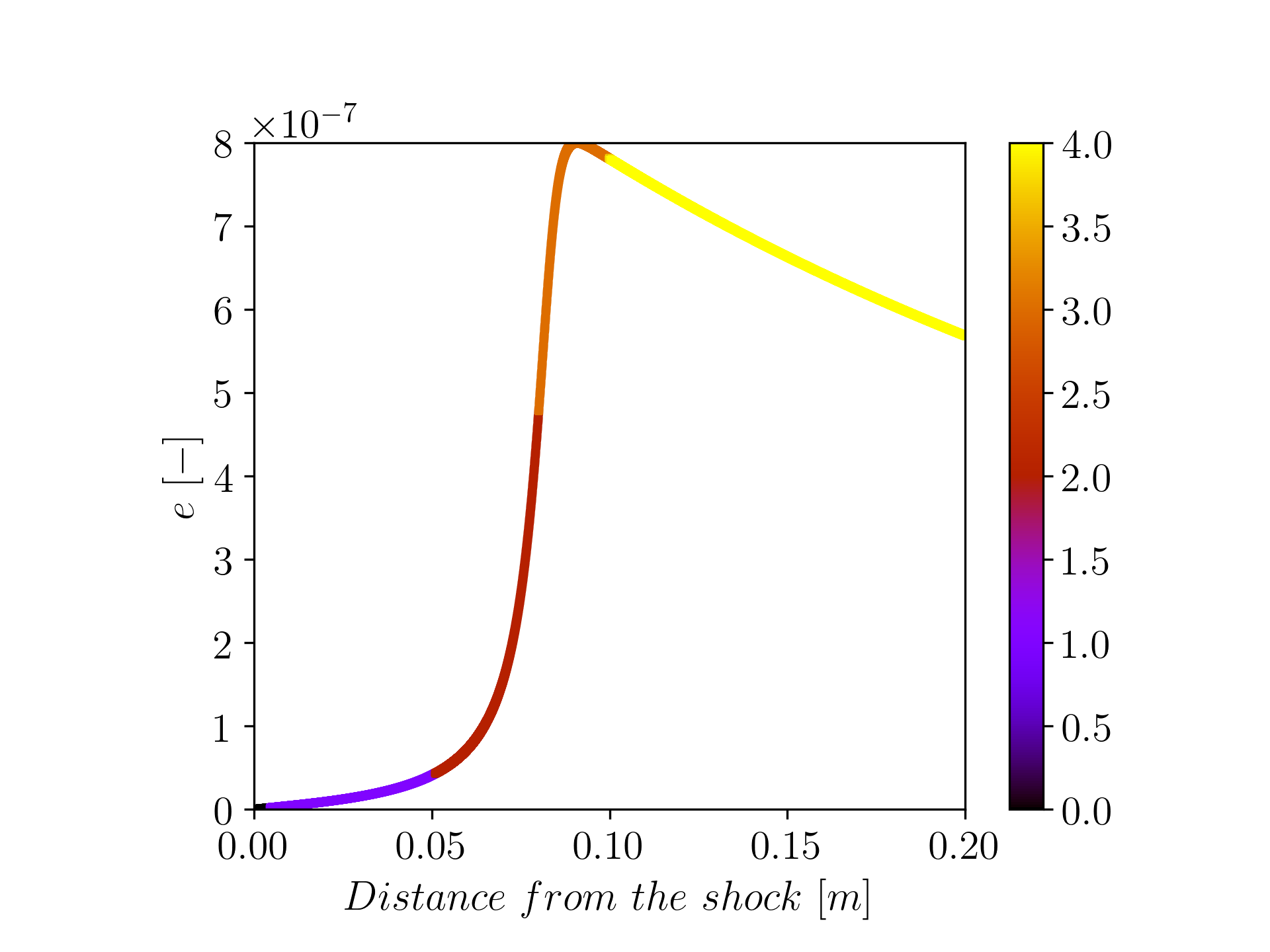
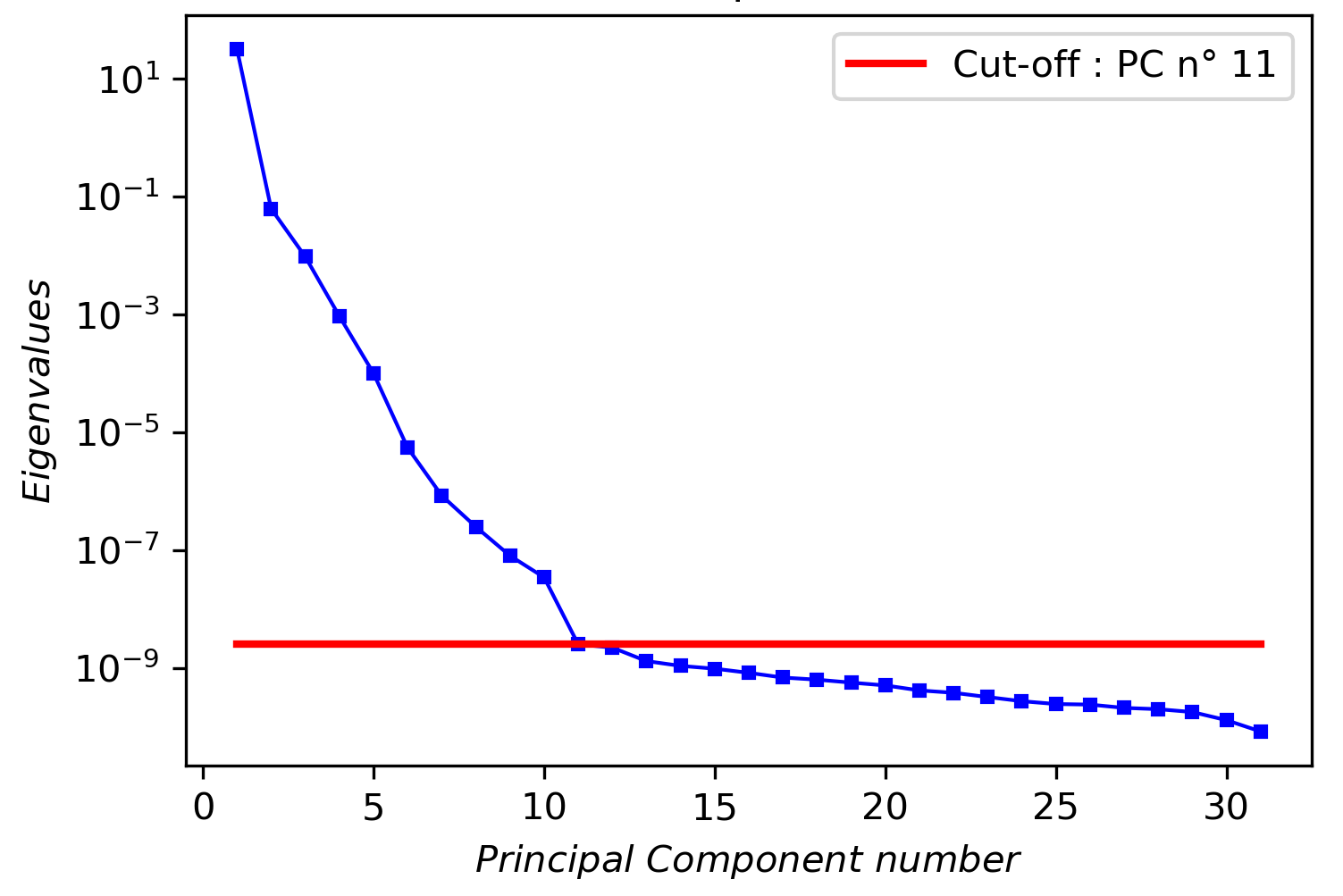
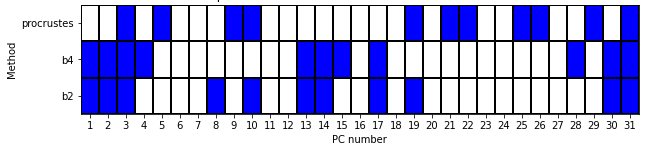
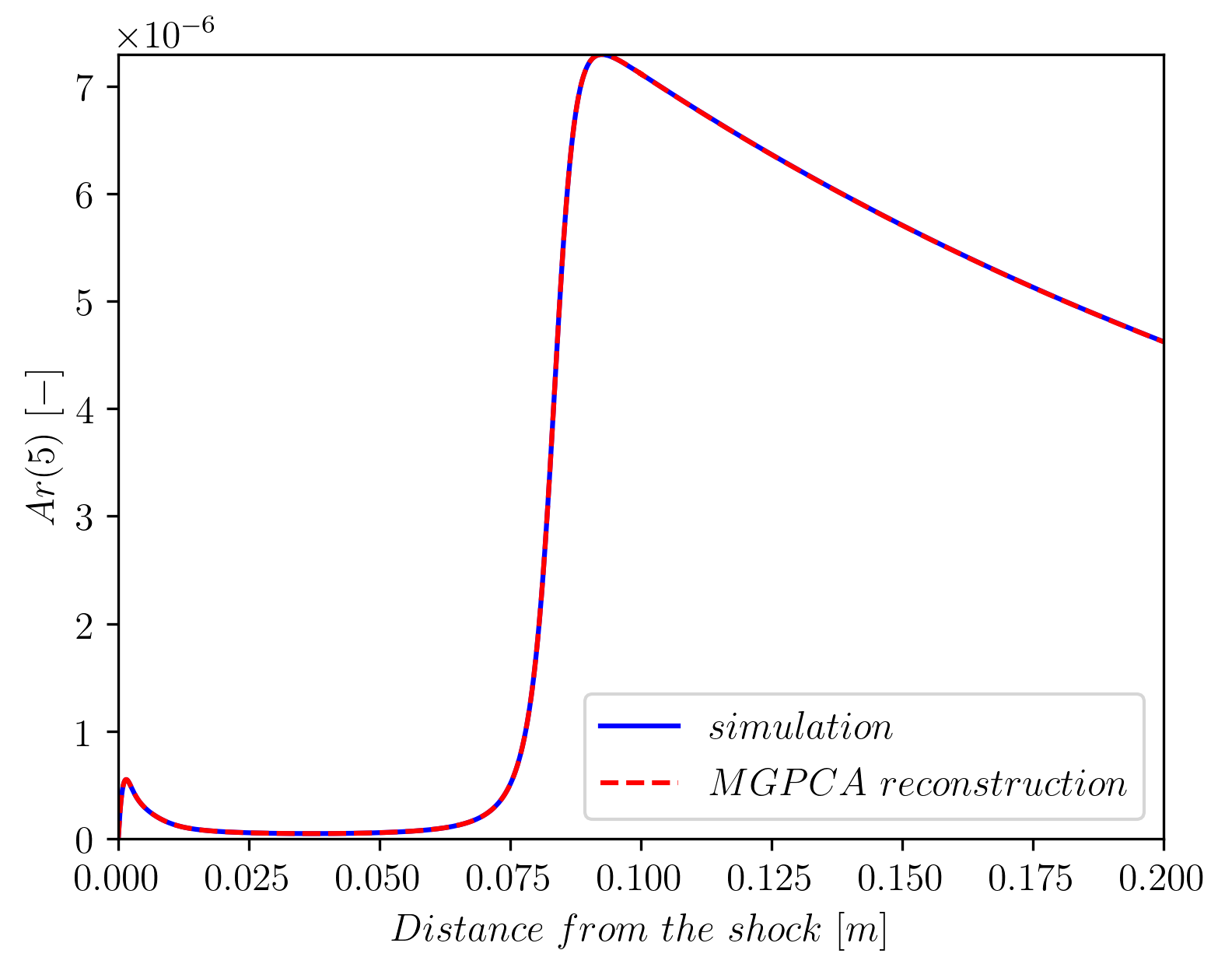
The next goal was to reduce the dimensionality of the data without significantly losing information, which is crucial for our subsequent Computational Fluid Dynamics (CFD) applications. While PCA can effectively project data into a lower-dimensional space, the resulting Principal Components (PC) are linear combinations of the entire dataset, which complicates their actual interpretation. What we would want is to construct this lower-dimensional space using a subset of the original variables, called Principal Variables (PV). To address this, I researched and implemented several methods and criteria for selecting the optimal number of principal components (PCs). Subsequently, I identified the Principal Variables (PVs) based on their significance according to my PCA analysis. The aim was to determine the minimal number of PVs that could achieve a reconstruction error below a specific threshold. Following that analysis, we are able to reconstruct the thermo-chemical states with a lower-dimensional manifold of only ~1/3 of the original variables (12 out of 34).