Convex MPC for Soft Landing

This project was accomplished as part of my Optimal Control & Reinforcement Learning class, taught by Pr. Zac Manchester.

This project reproduces the Powered-Descent Guidance algorithm used to solve the classical soft landing problem and embed the formulation within a Model Predictive Controller (MPC). I experimented with the controller under acceleration disturbances to reproduce real-world effects. The project repository is available here: Github Repository.

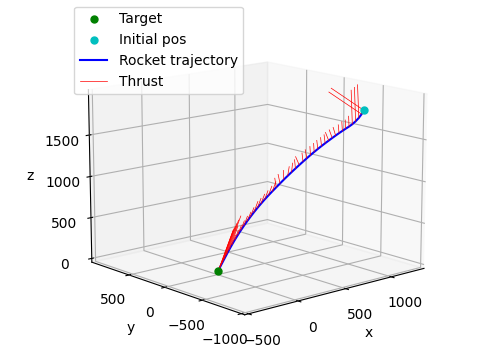
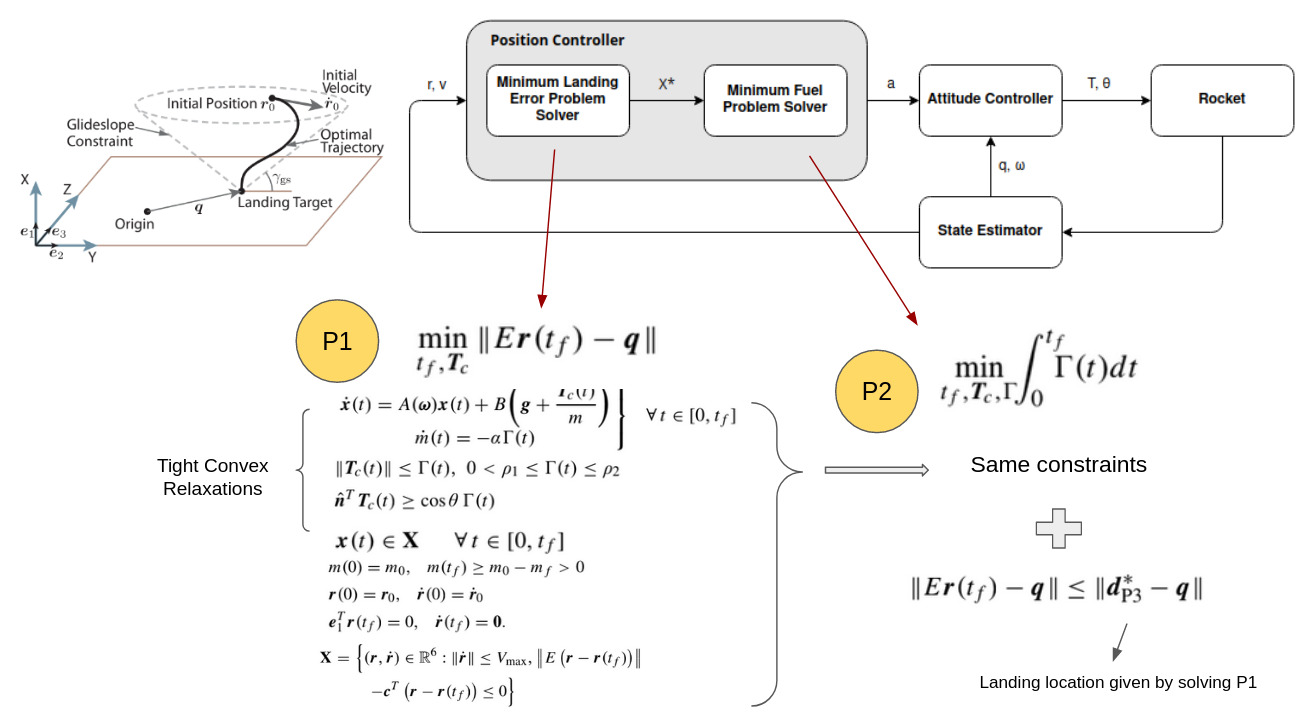
A depiction of a rocket trajectory (blue) with its thrust vector (red). The trajectory lasted 48s and the controller performed successfully under acceleration disturbances.

The MPC solves at each time step 2 subproblems: 1. a minimum landing error problem to get the maximum achievable landing position 2. a minimum-thrust problem to reach the found target position efficiently.

Abstract: Planetary soft landing is a crucial aspect of the Entry, Descent, and Landing (EDL) process for spacecraft, particularly with the growing number of scientific missions to outer planets and the need for reusable spacecraft. The Powered Descent Guidance (PDG) algorithm is an essential component of this process and can be expressed as a finite horizon optimal control problem with nonconvex state and control constraints. In this work, we utilize recent convexification techniques to facilitate onboard real-time computation of the PDG algorithm for the soft landing problem. By introducing a slack variable and a change of variable, we relax the nonconvex thrust bounds and pointing constraints and eliminate the nonlinearities in the dynamics. As a result, the original nonconvex problem is transformed into a convex problem where the optimal solution is also optimal for the original problem. We implement these algorithms using model predictive controllers, demonstrate their performance in the presence of disturbance, and highlight recursive feasibility problems. Finally, we propose potential avenues for improvement.

Report